I keep getting requests as to why I don't make the software tools I develop and use available for general use.  Since I am a research scientist, it was honestly never a primary goal to offer such a complex topic in a software. I used to do this with simulation and optimization software for complex dynamic systems with an open, freely definable mathematical model interface and noticed that such software is difficult to master, as over 98% of the "customer problems" at that time were caused by a lack of understanding of the respective mathematical and scientific relationships themselves. In other words, the skills required for the successful use of such software and the necessary maintenance are very high. The situation is similar with directed evolution. And as a research scientist with limited time, I want to use it to gain further knowledge and not "waste" it on maintaining the constantly changing software for each customers.
The tools developed can only be used in a licensed programming environment with additional libraries and only bring successful results to a pronounced specialist in this field and require knowledge-based, externally iteratively guided solution finding. At least when it comes to acoustic specialties.
Inspired by my work and the published approaches in the book "The Didgeridoo Phenomenon", a few years ago some interested parties reprogrammed my first ideas in open source. For example, DIDGMO or DIDJIMP. These versions can be used for simple specifications, but do not contain all the scientific know-how or directed evolution.

To give interested people an impression of how a typical CADSD process works, I would like to explain it below.

1. Desired specification:

The first step is to specify the desired instrument. This point seems simple at first. But anyone who tries to define their ideas about the sound and playability of an instrument will realize that it is not so easy to mathematically formulate the desired characteristics, which are often only vaguely describable, into hard physical targets. Therefore, it usually requires a good initial conversation to iteratively extract the physical goals for the instrument design based on the resulting answers.

Examples of specifications:

1. Basic drone
2. Sequence of toots
3. Playability of certain toots
4. Pseudo toots playable for experts
5. playable open flute notes
6. backpressure
7. emphasized prominent overtones (harmonics)
8. desired harmonic wobble pattern
9. Voice transmission behave
10. Amplification of certain heterodynes from basic tone and voice
11. Decay behave of the instrument

As described in the chapter "Acoustic fusions", specifications often call for characteristics or effects that are physically mutually exclusive and therefore cannot be realized. In principle, the following statement also applies:
The more effects are to be coupled in parallel in an instrument, the greater the playful and tonal flexibility of the instrument and the lower the typical expression of each individual effect.

2. Physical possibilities:

The given geometry of the inner shape of the instrument, i.e. the resulting vibrating air column, determines the sound and playing characteristics. In principle, only the position and height of the resulting intrinsic impedance peaks can be influenced within physically possible limits by the cross-sectional shape (geometry) of the inner form. And only the position and height of the available impedance peaks can influence all the properties described under specifications.
For example, a slightly conical instrument with a length of 125 cm has approx. 7-8 impedance peaks available in the range 0 - 1000 Hz. If the length is doubled to 250 cm, the number of impedance peaks doubles to 14-16.
For the realization of a specified property, the definition of the position and height of approx. 1-3 impedance peaks is required, depending on the property. This makes it clear that, as a rule, only the parallel realization of a limited combination of desired specified properties is possible. This means that if there are too many specified desired properties, it will be necessary to find the best compromise from the possible combination of properties that fulfills the specification.
 

The following rules must be observed:

1. The fundamental tone is usually approx. 2-3% above the frequency of the first input-impedance peak. The exact value depends, among other things, on the overall geometry of the instrument and the individual playing approach and can be influenced by experienced players.
2. The sequence of playable toots is determined by the position of the other input-impedance peaks.
3. The playability of the toots generally improves the higher the respective impedance peak is. It can be further improved the more overtones (harmonics) of the respective toot are underlaid by further impedance peaks. This increases the harmonicity of the respective toot and the impedance peaks used for this are no longer available to support other effects.
4. If a pseudo-toot that can be played by experts is to be realized within the first two octaves of the fundamental tone, the next 1-4 harmonics of the desired pseudo-toot frequency must be underlaid by the subsequent impedance peaks. However, this also limits their use for other effects.
5. In order to define playable open flute tones, the internal shape of the instrument must be selected so that the frequencies of the impedance minima (negative peaks) between the impedance peaks match the desired flute tones. This is possible, but it also limits the possibilities for placing the impedance peaks.
6. The noticeable back pressure of an instrument increases with the acoustic impedance at the mouthpiece. This is determined by the height of the respective impedance peak of the tone and its harmonicity. In order to achieve a high harmonicity, as many of the respective overtones (harmonics) of the tone played as possible must be underlaid by the subsequent impedance peaks. This also restricts the use of these impedance peaks for other effects.
7. In order to make certain harmonics more prominent, it is necessary to keep their output impedance at the bell end low (this maximizes the relative sound velocity at the bell end) in order to support the transmission of their sound energy to the environment. As a rule, the output impedance peaks at the bell end are often congruent with the impedance peaks we use, which are actually the input impedance peaks at the mouthpiece and say something about the playability of the notes in question. If these are kept relatively low, the audibility of the relevant overtones is generally improved. The disadvantage is that their playability as toots deteriorates as a result. However, this is not usually a problem, as the desired audible overtones are often in such a high frequency range where playable toots are not desired.
8. In principle, the same relationships described for more prominent audible harmonics also apply to more prominent perceptible harmonic wobbles. The only difference is that at least two desired harmonics are underlaid by two smaller impedance peaks that are symmetrically shifted 2-3% outwards.
9. The transmission behave of voice effects (e.g. imitation of animal voices), which is independent of the basic drone and the lower toots, can be improved if the impedance peaks in the range of approx. 800 - 2000 Hz are minimized. This minimizes the impedance formant of the vocal tract and allows the voice to unfold better. Large-volume instruments are usually better suited to this.
10. In order to support heterodyne tones consisting of a voice tone a fifth above the basic drone and this basic drone, any frequencies exactly from the mean value of the two neighboring overtone frequencies from the 2nd octave to the basic drone must be underlaid with an impedance peak. This means at the frequency ratios 5/2, 7/2, 9/2, 11/2, 13/2, 15/2, 17/2, ... (the smaller the ratios, the more effective);
11. The decay of an instrument becomes longer if the damping of the vibrating air column is minimized. This is usually possible with larger-volume instruments and a microscopically smooth inner surface. Furthermore, the decay behave is usually also extended in instruments with a relatively smooth cross-section without many steep constrictions. If there are too many constrictions, the vibration behave can deteriorate to such an extent that such instruments are difficult or even impossible to play.

3. Directed evolution process

With the CADSD method, it is in principle only possible to specify arbitrary internal shapes and calculate the sound and impedance spectra that can be generated with them. Unfortunately, it is not mathematically possible to set a target spectrum in advance and automatically calculate suggestions for corresponding internal shapes. To achieve this nevertheless, we developed our Didge(R)Evolution tool. This tool uses directed evolution algorithms to find the physically possible shapes to achieve the desired target spectra from the extremely high variety of possible shapes and generates suggestions for the best playable shapes. For this example shown here, approx. 1.2x10E144 shape variants are possible in the digital resolution used. Just for comparison, the number of atoms in the visible universe is approx. 1.0x10E88. This means that evolutionary algorithms are extremely efficient for complex tasks.
Since the solutions found in each case are unpredictable, it is usually necessary to test many alternative specifications that also lead to alternative solutions. Based on these solutions and an extensive knowledge base (which is not part of the software), the solution is then to found iteratively by the outside control by the specialist.
To illustrate this process, I will try to show a typical procedure using an example.

The internal shape for a Yidaki-type instrument with the following properties is to be found:

• a) Basic note F;
• b) 1st toot G1 and 2nd toot C2 (both easy and stable to play);
• c) 2nd overtone (3rd harmonic) C2 if possible more prominent audible;
• d) Heterodyne of voice tone C (fifth above basic note F) and basic tone F should be supported as on Mago-type instruments;
• e) Overtones 5, 6 and 7 (harmonics 6, 7 and 8) should be inducible as audible tones or harmonic wobbles, depending on the playing style;
• f) The instrument should have good acoustic elasticity when played;

The required physical parameters can now be derived on the basis of these desired specifications.
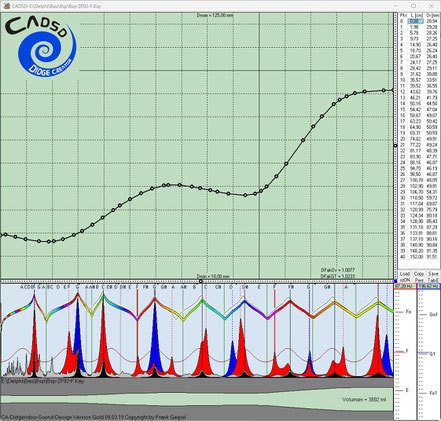
More important then the basic drone are all other desired properties , as these can be defined in relation to the fundamental tone from a physical point of view. The precise adjustment to the desired fundamental tone is usually carried out as the last transformative step. In principle, transformation to any fundamental tone is then possible. This proportional transformation sets the position of the first intrinsic impedance peak to the desired frequency of the fundamental tone (in our example to 87.31 Hz, fundamental tone F). All realized characteristics are retained.
In order to still land close to the desired fundamental F, we start the directional evolutionary search with a fixed length of 153 cm, as experience has shown that typical Yidaki instruments with fundamental F lie in this range.
Furthermore, we limit the search range of the directed evolution in an area where termites would naturally eat out an existing eucalyptus trunk. For this example, we use a version with 40 virtual segments and a total of 80 variable geometric parameters.

Derivation of the physical parameters:

• to a) fundamental F (1st impedance peak at 87.31 Hz related to 87.31 Hz -> ratio = 1.00);
• to b) 1st toot G1 (2nd impedance peak at 196.00 Hz in relation to 87.31 Hz -> ratio = 2.25); 2nd toot C2 (3rd impedance peak at 261.60 Hz in relation to 87.31 Hz -> ratio = 3.00); for good playability of the 1st and 2nd toots, impedance peaks 2 and 3 should have a defined minimum height.
  
• to c) The 2nd overtone (3rd harmonic) C2 should be supported by an impedance peak at 261.60 Hz (ratio 3.00 to the fundamental frequency). This goal is already defined by the desired position of the 2nd toot. Since the height of the 2nd impedance peak should have a defined minimum height for good playability of the 2nd toot, the sing tone will probably not be very prominent.  To achieve this, its height should be considerably lower, which would, however, lead to a deterioration in playability.
  
• to d) In order to support a heterodyne tone consisting of a voice tone of a fifth above the basic drone and this basic drone, any frequencies exactly from the mean value of the two neighboring overtone frequencies from the 2nd octave to the basic drone must be underlaid with an impedance peak. So at the frequency ratios 5/2, 7/2, 9/2, 11/2, 13/2, 15/2, 17/2, ... (the smaller the ratios, the more effective); So, since the position of the first 3 impedance peaks is already assigned and we want to support the mixed tone (heterodyne) of voice tone C (fifth above fundamental F) and fundamental F as in Mago-type instruments, we set the 4th impedance peak to the ratio 9/2 = 4.5;
  
• to e) Overtones 5, 6 and 7 (harmonics 6, 7 and 8) should be excitable as singing tones or harmonic wobbles, depending on the playing style. To achieve this, we underlay these three overtones with the impedance peaks 5, 6 and 7. To achieve a symmetrical pattern, we place the impedance peak 6 under the middle (central) overtone 6 and place the impedance peak 5 approx. 2-3% to the left of the frequency of overtone 5 and the impedance peak 7 approx. 2-3% to the right of the frequency of overtone 7. This should allow overtone 6 to be perceived as a singing tone when playing stationary and overtones 5 and 7 to be stimulated alternately for harmonic wobbling when playing dynamically in the traditional way. In order to achieve a good perception of these overtones, which is ensured by a good transmission of the sound energy of these overtones from the bell end, the height of the respective underlying impedance peaks must not be too high.
  Ratios of impedance peaks 5, 6, 7 to the fundamental F 87.31 Hz:
  Impedance peak 5: approx. 2.5% below overtone 5 -> 510.8 Hz / 87.31 Hz -> ratio 5.85
  Impedance peak 6: overtone 6 -> 611.2 Hz / 87.31 Hz -> ratio 7.00
  Impedance peak 7: approx. 2.5% above overtone 7 -> 711.6 Hz / 87.31 Hz -> ratio 8.15
  
• to f) The impedance peaks 5 and 7 are offset symmetrically by approx. 2-3% in relation to the harmonics 5 and 7, giving the instrument a good acoustic elasticity. This can be further improved by placing the two following impedance peaks 8 and 9 also approx. 2-3% to the left of overtone 8 (harmonic 9) and approx. 2-3% to the right of overtone 9 (harmonic 10). For reasons of better audibility and voice transmission in this high frequency range, the height of the underlying impedance peaks is also limited.
  Ratios of the impedance peaks 8, 9 to the fundamental F 87.31 Hz:
  Impedance peak 8 approx. 2% below overtone 8 -> 855.6 Hz / 87.31 Hz -> ratio 9.80
  Impedance peak 9: approx. 2% above overtone 9 -> 977.9 Hz / 87.31 Hz -> ratio 11.20
  

In order to quantitatively transfer (provide) these physical parameters derived from the specification into the algorithms of the directed evolutionary search, 19 functions are currently available for target definition.

This provision leads to the following 15 search objectives for the directed evolution, to which the minimization of the weighted sum of the angles between the segments is added as an additional objective. This additional goal means that the "smoothest" inner shape is always selected from the theoretically infinite number of possible solutions, which experience has shown to be the most playable.

In the version of directed evolution currently in use, up to 20 parallel search targets are possible.

Run of a directed evolution:

Since very few people interested in didgeridoo building are familiar with mathematical modeling, programming and physical theories, here is a simplified description of how it works:

• Imagine we create (program) virtual termite colonies whose individual termites have individual abilities to form didgeridoos with special characteristics. The first step is to determine the size and number of these virtual termite colonies. In our example, we only work with one colony (population) consisting of 512 termites (individuals).
• Within the spatial boundary of the virtual blank (the search area), each individual termite starts its work and eats its own didgeridoo (initially completely randomly). After a few seconds the first 512 virtual instruments are ready.
• Each individual instrument is now tested on the basis of the simulated/calculated impedance and sound spectra to see how well it fulfills the specified target properties. The termites that were most successful are allowed to reproduce and pass on their genetic information to a new generation of termites. The others die out. This means that the most successful virtual instruments remain in the pool and are used as starting instruments for the modification of further forms. In addition, as in nature, random mutations are generated that change the individual characteristics of individual termites (instruments). This concludes the first generation.
• In the second generation, the offspring, together with their relatively successful parents and the mutated siblings, again eat out 512 didgeridoo blanks - again randomly controlled but with improved characteristics to achieve the targets. Behind this is a series of different mathematical operators that mix and recombine the existing information according to the known laws of genetic algorithms, for example, in such a way that a new generation of virtual instruments is created that should statistically lead to a high probability of better fulfillment of the targets.
• All instruments are then checked again. The successful termites (virtual instruments) of the population (instrument pools) are allowed to reproduce again, while the rest die out (as already described in the previous generation).
• This evolutionary cycle continues until a virtual didgeridoo has been created that fulfills all the predefined goals in the best possible way and there is no more evolutionary progress - visible as a red line in the example. This is usually the case after 150 to 400 generations. The current typical time for a modern single processor is 10-30 minutes.

In order to prevent directed evolution from becoming bogged down by too many targets, one usually starts with fewer targets, which are then gradually extended to the overall targets on the basis of observed evolution and one's own experience. As the supervisor of the directed evolution (in this case me) can follow the development of the results graphically, the step-by-step extensions or modifications are already prepared during active runs and started in parallel to the runs already running. Runs that are not promising are aborted. In this phase, up to approx. 30 parallel runs on 30 processors are possible with my current technology. This means that, especially in complicated projects, I am currently still an essential part of this global optimization with the help of directed artificial evolution. As every global search is different and often unpredictable, this process remains exciting to this day.
Typical development times range from around an hour for simpler projects to several days for complicated complex projects, even with automatic runs overnight. Once the best and physically suitable target combination has been found, the final runs often involve several thousand generations in order to find the best one from the multitude of possible shapes based on current experience. In our example, there are 2200 generations each.
All variants of the tools I use currently consist of approx. 30000 lines of source code, of which approx. 20000 lines are for the search using directed artificial evolution algorithms and approx. 10000 lines for the subsequent manual modification in the Didge-Creator.

Here are some screenshots during the runs of our described example:

Here, 6 Evo runs were started in parallel, with the number of defined individual targets increasing from 2, 3, 4, 7, 9 to 16 from left to right. The height of the yellow individual bars gives a graphic impression of how far away an individual goal is from being fully achieved.

Here are the same Evo runs a few generations further on:

The thin curves (yellow, light blue and green) in the dark blue windows sloping to the left show the approach or convergence to the overall target of zero deviation at two power-of-ten intervals. In the following screenshots you can see that the more individual targets and the more complex they are, the slower the Evo-Runs converge to the overall target of zero deviation.
If the individual goals contradict each other or are physically unattainable, the respective Evo run converges with a relatively large residual deviation from zero. In this example, the experience-based target definition provides a solution for each Evo run.

Here you can better recognize the thin curves (yellow, light blue and green) in the dark blue windows that slope to the left. These show the approximation or convergence to the overall target of zero deviation at two power-of-ten intervals. The more individual targets and the more complex they are, the slower the evo runs converge to the overall target of zero deviation.

Discussion of the individual results of Evo-Runs 1-6 after 2200 generations each:

If you look closely at the results, you can see that the targets were all reached relative to the first impedance peak (the basic drone), but the frequency of this first impedance peak still needs to be adjusted to the desired fundamental frequency F at 87.31 Hz. This was to be expected and is normal, as the fundamental frequency depends not only on the length (in this case 153 cm), but also on the entire internal geometry of the instrument.
We use the Didge-Creator for these adjustments, transformations and fine tuning.

4. Transformation with the Didge-Creator:

First of all, it should be noted that the pitch of the fundamental tone to be set also depends on a number of parameters. On the one hand, these are physical parameters independent of the player, such as temperature gradient and humidity in the instrument. This alone can result in deviations of up to half a tone. It makes a clear difference whether you play in the tropics at >30°C and maximum humidity or in a temperate zone at 18°C and lower humidity. The influence of temperature is greater than that of humidity. All in all, this influence has no effect on the overall characteristics of the instrument, as the change in sound velocity in the instrument affects all relevant variables in the same way and the changes caused by this are only relative.
On the other hand, there are the parameters that depend on the individual player. These include the lip connection to the mouthpiece and the associated lip tension and playing pressure. Depending on the internal shape of the instrument, this can also cause the fundamental frequency to fluctuate by up to a quarter tone. Experienced players also consciously use these effects to vary the fundamental tone up to a whole tone, for example. With regard to certain overtone effects (e.g. singing tones, harmonic wobbles), these dependencies must be evaluated more critically, as they influence the overall characteristics of the instrument. This is also one of the main reasons why a relatively large number of players fail to develop potentially available singing tone or harmonic wobble qualities. In these cases, it would be necessary to fine-tune the instrument to the player, so that these effects can be stimulated for the individual player. Another reason for the perception or non-perception of certain harmonic effects is the training of one's own acoustic perception. This can be learned and practiced. However, as with other activities, there are people who have a particularly strong talent for this and others less so.
However, one of the most important prerequisites for stimulating potential harmonic wobbles, for example, is mastering a suitable playing technique and thus conscious interaction with the instrument. The various traditional playing techniques in balance with the instrument are particularly suitable for this.
As interesting and entertaining as more modern playing techniques such as beatboxing are, these techniques usually lead to the acoustic "rape" of an instrument, whereby the acoustic properties of the instrument no longer play such an important role, as the player is the most important sound-producing aspect here and therefore a relatively arbitrary tube is often sufficient. Unfortunately, most slide instruments also fall into this category. These have the advantage for musicians of being able to adjust the fundamental tone in any situation. However, the overall characteristics of these instruments change with every adjustment. As a result, there is usually only one setting for an acoustic "sweet spot" for experienced players and listeners, but most listeners will probably not notice this in their typical use.

Transformation of instruments to other pitches:

Since the instrument from Evo-Run 1 has some unplanned additional qualities, I will use this instrument to demonstrate the procedure.

Concluding remark:

That was a lot of material for hardcore Didge physics enthusiasts. I hope that people interested in this topic have gained an insight into what I do with CADSD and that I was able to answer some open questions.

With best regards
Frank Geipel, June 16, 2024